[Data Structure] 이진 탐색 트리(Binary Search Tree) 개념 및 구현
이진 탐색 트리(Binary Search Tree)
이진 탐색 트리(Binary Search Tree)는 트리 자료구조의 한 종류로 노드의 차수가 0~2로 자식 노드가 최대 두 개까지만 허용되는 트리이다.
이진 트리와 다르게 부모 노드를 기준으로 작은 값은 왼쪽 노드에 저장되고 큰 값은 오른쪽 노드에 저장된다.

이진 탐색 트리의 특징
이진 탐색 트리는 기본적으로 이진 트리에 데이터의 대소를 비교하여 왼쪽이나 오른쪽 노드에 저장하게 된다. 탐색을 목적으로 한 자료구조이기 때문에 데이터의 중복을 허용하지 않는다.
트리에 데이터가 한쪽 방향으로만 저장되는 경우엔 탐색 속도는 O(N), 포화 이진 트리의 경우 탐색 속도는 O(logN)이다.
중위순회(inorder traversal) 방법으로 순회한다.
이진 탐색 트리 삽입
이진 탐색 트리는 데이터가 부모 노드보와 대소 비교하여 왼쪽 또는 오른쪽으로만 가기 때문에 루트 노드부터 비교하며 자리를 찾아가면 된다.
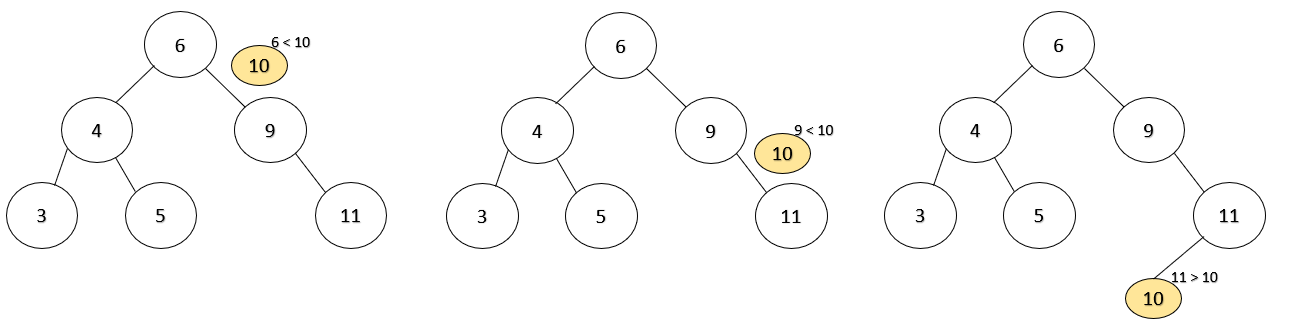
이진 탐색 트리 탐색
탐색의 경우엔 삽입과 마찬가지로 데이터의 값을 비교하며 내려간다. 데이터가 트리에 없으면 끝까지 내려가고 탐색을 종료한다.
이진 탐색 트리 삭제
삭제의 경우엔 삽입과 탐색보다 까다롭다.
삭제는 3가지 경우를 고려해야 한다.
1. 삭제하는 노드가 리프 노드일 경우
2. 삭제하는 노드의 자식 노드가 1개일 경우
3. 삭제하는 노드의 자식 노드가 2개일 경우
1. 삭제하는 노드가 리프 노드일 경우
제일 간단한 경우이다. 이 경우엔 부모 노드의 관계를 끊어주면 된다.

트리에서 11을 지우는 경우 11은 자식 노드가 없는 리프 노드이다. 부모 노드의 오른쪽 자식을 null로 변경하면 끝난다.
2. 삭제하는 노드의 자식 노드가 1개일 경우
삭제하는 노드의 부모 노드와 삭제하는 노드의 자식 노드를 연결시켜줘야 한다.

3. 삭제하는 노드의 자식 노드가 2개일 경우
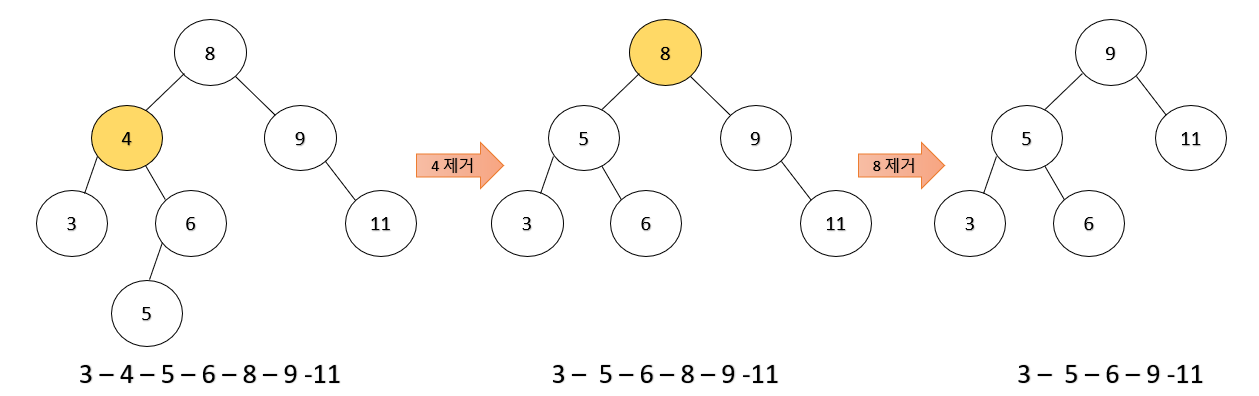
자식 노드가 2개인 경우엔 삭제하는 노드의 오른쪽 서브 트리에서 가장 작은 값을 찾아야 한다. 이 노드를 successor라고 하는데, 삭제하는 노드의 자리를 이 successor가 대체한다. successor를 찾는 이유는 기본적으로 이진 트리 탐색은 값의 대소를 비교하여 저장하기 때문에 중위 순회를 돌 때 데이터의 순서가 유지되게 하기 위함이다.

노드가 삭제되기 전에 순회 경로를 보면 3 - 4 - 5 - 6 - 8 - 9 - 11 순으로 도는데 여기서 4를 제거하고 successor로 자리를 대신하면 3 - (4) - 5 - 6 - 8 - 9 - 11로 순서가 유지되는 것을 확인할 수 있다.
이진 탐색 트리 구현
이진 탐색 트리를 구현해보면서 여러 가지 케이스를 생각해야 돼서 까다로웠다. 여러 케이스를 테스트해보면서 구현했지만 오류가 있을 수 있다...
Node
public class Node {
private int data;
private Node left;
private Node right;
public Node(int data) {
this.data = data;
this.left = null;
this.right = null;
}
public int getData() {
return data;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
}
BinarySearchTree()
public class BinarySearchTree {
private Node root;
private int size;
public BinarySearchTree() {
root = null;
size = 0;
}
}
add()
public boolean add(int data){
Node newNode = new Node(data);
if(root == null){ //트리가 비어있을 경우
root = newNode;
size++;
return true;
}
if(root.getData() == data){ //데이터 중복
return false;
}
Node curNode = root;
Node parentNode = null;
while(curNode != null){ //루트부터 데이터 넣을 자리 탐색
parentNode = curNode;
if(curNode.getData() > data){
curNode = curNode.getLeft();
if(curNode == null){
parentNode.setLeft(newNode);
break;
}else if(curNode.getData() == data){
return false;
}
}else {
curNode = curNode.getRight();
if(curNode == null){
parentNode.setRight(newNode);
break;
}else if(curNode.getData() == data){
return false;
}
}
}
size++;
return true;
}삽입될 데이터를 루트부터 대소 비교를 하면서 놓일 자리를 탐색한다. 탐색하면서 비어있는 자리를 찾으면 parentNode와 관계를 설정해준다.
contain()
public boolean contain(int data){
Node curNode = root;
while(curNode != null){
if(curNode.getData() == data){
return true;
}
if(curNode.getData() > data){
curNode = curNode.getLeft();
}else {
curNode = curNode.getRight();
}
}
return false;
}루트 노드부터 탐색해서 트리에 데이터가 있는지 boolean 타입으로 반환
remove()
remove 메서드는 코드가 길어서 앞에 설명한 3가지 경우를 나눠서 작성하겠다. 전체 코드는 마지막에 있다.
public boolean remove(int data){
if(root == null || !contain(data)){
return false;
}
Node parentNode = null;
Node currentNode = root;
boolean isLeft = true;
//노드 찾기
while(currentNode.getData() != data){
parentNode = currentNode;
if(currentNode.getData() > data){
isLeft = true;
currentNode = currentNode.getLeft();
}else {
isLeft = false;
currentNode = currentNode.getRight();
}
}
리프 노드인 경우
if(currentNode.getLeft() == null && currentNode.getRight() == null){ //리프노드인 경우
if(currentNode == root){
root = null;
size = 0;
return true;
}
if(isLeft){
parentNode.setLeft(null);
}else {
parentNode.setRight(null);
}
currentNode = null;
}앞에서 탐색하면서 isLeft를 사용해서 제거될 노드가 부모 노드의 왼쪽 자식인지 오른쪽 자식인지 확인했다. 왼쪽 자식이면 부모 노드의 왼쪽을 null로 변경하고 오른쪽 자식이면 오른쪽 노드를 null로 변경해서 관계를 끊어준다.
자식 노드가 하나인 경우
else if(currentNode.getLeft() == null){
if(currentNode == root){
root = currentNode.getRight();
currentNode = null;
}else {
if(!isLeft){
parentNode.setRight(currentNode.getRight());
}else{
parentNode.setLeft(currentNode.getRight());
}
currentNode = null;
}
}else if(currentNode.getRight() == null){
if(currentNode == root){
root = currentNode.getLeft();
currentNode = null;
}else {
if(!isLeft){
parentNode.setRight(currentNode.getLeft());
}else{
parentNode.setLeft(currentNode.getLeft());
}
currentNode = null;
}
}제거되는 노드의 보무 노드, 자식 노드의 관계를 맺어준다.
자식 노드가 두 개인 경우
자식 노드가 두 개인 경우엔 successor를 찾아야 한다고 했다.
successor와 successor의 부모를 찾는 메서드 먼저 봐야 할 것 같다.
private Node getParentOfSuccessor(Node node,int data){
if(node == null){
return null;
} else if (node.getData() < data){
if(node.getRight() != null){
if (node.getRight().getData() == data){
return node;
}else {
return getParentOfSuccessor(node.getRight(),data);
}
} else{
return null;
}
} else if (node.getData() > data){
if(node.getLeft() != null){
if(node.getLeft().getData() == data){
return node;
}else {
return getParentOfSuccessor(node.getLeft(),data);
}
}else {
return null;
}
}
return null;
}
private Node getSuccessor(Node node){
if(node.getLeft() == null){
return node;
} else{
return getSuccessor(node.getLeft());
}
}successor는 오른쪽 서브 트리에서 가장 작은 값이라고 했다. remove 메서드에서 제거되는 노드의 오른쪽 자식으로 메서드를 호출하기 때문에 이 메서드에선 왼쪽 노드를 계속해서 재귀적으로 호출한다. 이제 다시 remove 메서드로 돌아가자.
else {
Node successor = getSuccessor(currentNode.getRight());
Node parentOfSuccessor = getParentOfSuccessor(root, successor.getData());
if(currentNode == root){
if(parentOfSuccessor == currentNode){
root = successor;
root.setLeft(currentNode.getLeft());
currentNode = null;
} else {
parentOfSuccessor.setLeft(successor.getRight());
root = successor;
root.setLeft(currentNode.getLeft());
root.setRight(currentNode.getRight());
currentNode = null;
}
} else {
if(!isLeft){
parentNode.setRight(successor);
successor.setLeft(currentNode.getLeft());
if(currentNode.getRight() != successor){
if(successor.getRight() != null) {
parentOfSuccessor.setLeft(successor.getRight());
}else {
parentOfSuccessor.setLeft(null);
}
successor.setRight(currentNode.getRight());
}
currentNode = null;
} else{
parentNode.setLeft(successor);
successor.setLeft(currentNode.getLeft());
if(currentNode.getRight()!= successor){
if(successor.getRight() != null) {
parentOfSuccessor.setLeft(successor.getRight());
}else {
parentOfSuccessor.setLeft(null);
}
successor.setRight(currentNode.getRight());
}
currentNode = null;
}
}
}
size--;
return true;successor와 successor의 부모 노드를 찾고 이를 이용해서 제거되는 노드의 부모 노드와, 자식 노드들 간에 관계를 맺어준다.
inorder()
public void inorder(Node root,int depth){
if(root != null){
inorder(root.getLeft(),depth + 1);
System.out.print(root.getData() + " ");
inorder(root.getRight(),depth+1);
}
}
중위 순회 방식으로 트리 출력
Test
위의 과정으로 테스트
public class Main {
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree();
bst.add(8);
bst.add(4);
bst.add(9);
bst.add(11);
bst.add(3);
bst.add(6);
bst.add(5);
bst.inorder(bst.getRoot(),0);
System.out.println();
bst.remove(4);
bst.inorder(bst.getRoot(),0);
System.out.println();
bst.remove(8);
bst.inorder(bst.getRoot(),0);
System.out.println();
}
}
BinarySearchTree 전체 코드
public class BinarySearchTree {
private Node root;
private int size;
public BinarySearchTree() {
root = null;
size = 0;
}
public boolean add(int data){
Node newNode = new Node(data);
if(root == null){
root = newNode;
size++;
return true;
}
if(root.getData() == data){
return false;
}
Node curNode = root;
Node parentNode = null;
while(curNode != null){
parentNode = curNode;
if(curNode.getData() > data){
curNode = curNode.getLeft();
if(curNode == null){
parentNode.setLeft(newNode);
break;
}else if(curNode.getData() == data){
return false;
}
}else {
curNode = curNode.getRight();
if(curNode == null){
parentNode.setRight(newNode);
break;
}else if(curNode.getData() == data){
return false;
}
}
}
size++;
return true;
}
public boolean remove(int data){
if(root == null || !contain(data)){
return false;
}
Node parentNode = null;
Node currentNode = root;
boolean isLeft = true;
while(currentNode.getData() != data){
parentNode = currentNode;
if(currentNode.getData() > data){
isLeft = true;
currentNode = currentNode.getLeft();
}else {
isLeft = false;
currentNode = currentNode.getRight();
}
}
if(currentNode.getLeft() == null && currentNode.getRight() == null){
if(currentNode == root){
root = null;
size = 0;
return true;
}
if(isLeft){
parentNode.setLeft(null);
}else {
parentNode.setRight(null);
}
currentNode = null;
}else if(currentNode.getLeft() == null){
if(currentNode == root){
root = currentNode.getRight();
currentNode = null;
}else {
if(!isLeft){
parentNode.setRight(currentNode.getRight());
}else{
parentNode.setLeft(currentNode.getRight());
}
currentNode = null;
}
}else if(currentNode.getRight() == null){
if(currentNode == root){
root = currentNode.getLeft();
currentNode = null;
}else {
if(!isLeft){
parentNode.setRight(currentNode.getLeft());
}else{
parentNode.setLeft(currentNode.getLeft());
}
currentNode = null;
}
}else {
Node successor = getSuccessor(currentNode.getRight());
Node parentOfSuccessor = getParentOfSuccessor(root, successor.getData());
if(currentNode == root){
if(parentOfSuccessor == currentNode){
root = successor;
root.setLeft(currentNode.getLeft());
currentNode = null;
} else {
parentOfSuccessor.setLeft(successor.getRight());
root = successor;
root.setLeft(currentNode.getLeft());
root.setRight(currentNode.getRight());
currentNode = null;
}
} else {
if(!isLeft){
parentNode.setRight(successor);
successor.setLeft(currentNode.getLeft());
if(currentNode.getRight() != successor){
if(successor.getRight() != null) {
parentOfSuccessor.setLeft(successor.getRight());
}else {
parentOfSuccessor.setLeft(null);
}
successor.setRight(currentNode.getRight());
}
currentNode = null;
} else{
parentNode.setLeft(successor);
successor.setLeft(currentNode.getLeft());
if(currentNode.getRight()!= successor){
if(successor.getRight() != null) {
parentOfSuccessor.setLeft(successor.getRight());
}else {
parentOfSuccessor.setLeft(null);
}
successor.setRight(currentNode.getRight());
}
currentNode = null;
}
}
}
size--;
return true;
}
public Node getRoot() {
return root;
}
private Node getParentOfSuccessor(Node node,int data){
if(node == null){
return null;
} else if (node.getData() < data){
if(node.getRight() != null){
if (node.getRight().getData() == data){
return node;
}else {
return getParentOfSuccessor(node.getRight(),data);
}
} else{
return null;
}
} else if (node.getData() > data){
if(node.getLeft() != null){
if(node.getLeft().getData() == data){
return node;
}else {
return getParentOfSuccessor(node.getLeft(),data);
}
}else {
return null;
}
}
return null;
}
private Node getSuccessor(Node node){
if(node.getLeft() == null){
return node;
} else{
return getSuccessor(node.getLeft());
}
}
public boolean isEmpty() {
return root == null;
}
public int size() {
return size;
}
public boolean contain(int data){
Node curNode = root;
while(curNode != null){
if(curNode.getData() == data){
return true;
}
if(curNode.getData() > data){
curNode = curNode.getLeft();
}else {
curNode = curNode.getRight();
}
}
return false;
}
public void inorder(Node root,int depth){
if(root != null){
inorder(root.getLeft(),depth + 1);
System.out.print(root.getData() + " ");
inorder(root.getRight(),depth+1);
}
}
}
'Computer Science > 알고리즘 & 자료구조' 카테고리의 다른 글
| [Data Structure] 트리(Tree), 이진 트리(Binary Tree) (0) | 2022.09.28 |
|---|---|
| [Data Structure] 큐 (Queue)개념 및 구현 (0) | 2022.09.27 |
| [Data Structure] 연결 리스트 (LinkedList)개념 및 구현 (0) | 2022.09.26 |
| [Data Structure] 스택 (Stack)개념 및 구현 (0) | 2022.09.23 |
| [Algorithm] 재귀 함수 (Recursive Function) (0) | 2022.09.21 |













